Implementing Recurrent Neural Network
BDA 492 Project
Submitted By: Agastya Seth
Recurrent Neural Network
What is a Recurrent Network?
A recurrent neural network (RNN) is a class of artificial neural network where connections between nodes form a directed graph along a sequence. This allows it to exhibit temporal dynamic behavior for a time sequence. Unlike feedforward neural networks, RNNs can use their internal state (memory) to process sequences of inputs. This makes them applicable to tasks such as unsegmented, connected handwriting recognition or speech recognition.
Feedforward networks are great for learning a pattern between a set of inputs and outputs.



This includes problems like predicting:
- temperature & location
- height & weight
- car speed and brand
But what these networks fail to incorporate is the order of the inputs. There are many cases where the order of the data really matters:

Just like how when we learn the Alphabet, Lyrics of a song. These are stored using Conditional Memory. We can only access an element if you have access to the previous elements (like a linked-list).
Enter recurrent networks
We feed the hidden state from the previous time step back into the the network at the next time step.
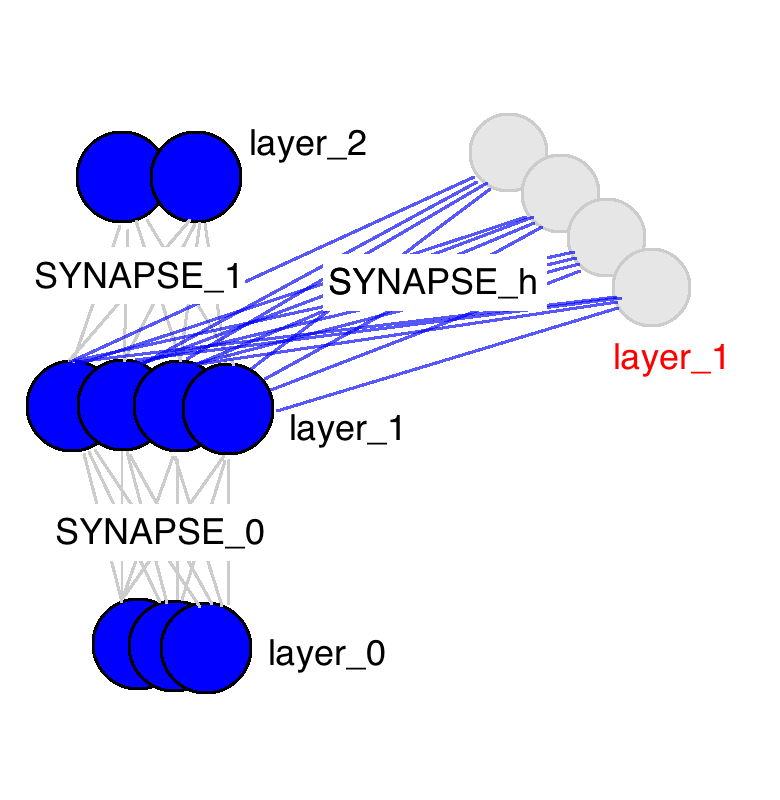
So instead of the data flow operation happening like this
input -> hidden -> output
it happens like this
(input + prev_hidden) -> hidden -> output
Why not this?
(input + prev_input) -> hidden -> output
Hidden recurrence learns what to remember whereas input recurrence is hard wired to just remember the immediately previous datapoint


RNN Formula

It basically says the current hidden state h(t) is a function f of the previous hidden state h(t-1) and the current input x(t). The theta are the parameters of the function f. The network typically learns to use h(t) as a kind of lossy summary of the task-relevant aspects of the past sequence of inputs up to t.
Loss function
The total loss for a given sequence of x values paired with a sequence of y values would then be just the sum of the losses over all the time steps. For example, if L(t) is the negative log-likelihood of y (t) given x (1), . . . , x (t) , then sum them up you get the loss for the sequence
Our steps
- Initialize weights randomly
- Give the model a char pair (input char & target char. The target char is the char the network should guess, its the next char in our sequence)
- Forward pass (We calculate the probability for every possible next char according to the state of the model, using the paramters)
- Measure error (the distance between the previous probability and the target char)
- We calculate gradients for each of our parameters to see their impact they have on the loss (backpropagation through time)
- update all parameters in the direction via gradients that help to minimise the loss
- Repeat! Until our loss is small (as per a threshold)
What are some use cases?
- Time series prediction (weather forecasting, stock prices, traffic volume, etc. )
- Sequential data generation (music, video, audio, etc.)
The code contains 4 parts
- Load the trainning data
- encode char into vectors
- Define the Recurrent Network
- Define a loss function
- Forward pass
- Loss
- Backward pass
- Define a function to create sentences from the model
- Train the network
- Feed the network
- Calculate gradient and update the model parameters
- Output a text to see the progress of the training
Load the training data
The network needs a big .txt file as an input.
The content of the file will be used to train the network.
I used the book Methamorphosis from Kafka, as it’s probably one of my favorite books I found on Public Domain.
data = open('kafka.txt', 'r').read()
chars = list(set(data))
data_size, vocab_size = len(data), len(chars)
print ('data has %d chars, %d unique' % (data_size, vocab_size))
data has 137628 chars, 80 unique
Encode/Decode char/vector
Neural networks operate on vectors (a vector is an array of float) So we need a way to encode and decode a char as a vector.
We’ll count the number of unique chars (vocab_size). That will be the size of the vector. The vector contains only zero exept for the position of the char wherae the value is 1.
So First let’s calculate the vocab_size:
char_to_ix = { ch:i for i,ch in enumerate(chars)}
ix_to_char = { i:ch for i, ch in enumerate(chars)}
print (char_to_ix)
print (ix_to_char)
{'P': 0, 'n': 1, 'm': 2, 'v': 3, '"': 4, "'": 5, 'T': 6, 'V': 7, '8': 8, '?': 9, '%': 10, 'S': 11, '0': 12, 'u': 13, 'R': 14, '$': 15, 'd': 16, 'M': 17, '2': 18, 'F': 19, 'p': 20, 'b': 21, '-': 22, 'D': 23, 'y': 24, '.': 25, ':': 26, '(': 27, 'X': 28, 'o': 29, 'k': 30, 'j': 31, 'ç': 32, '@': 33, 'l': 34, '\n': 35, 'W': 36, 'C': 37, '5': 38, 'i': 39, 'O': 40, '6': 41, 'z': 42, '9': 43, ')': 44, '4': 45, 'G': 46, 'c': 47, 'A': 48, 'U': 49, 'L': 50, '*': 51, 'J': 52, 'x': 53, ',': 54, 'Q': 55, 's': 56, 't': 57, 'Y': 58, 'a': 59, 'g': 60, 'B': 61, 'e': 62, 'H': 63, 'q': 64, 'r': 65, 'K': 66, '7': 67, '3': 68, '!': 69, 'w': 70, '1': 71, 'f': 72, 'I': 73, 'E': 74, 'N': 75, 'h': 76, ';': 77, ' ': 78, '/': 79}
{0: 'P', 1: 'n', 2: 'm', 3: 'v', 4: '"', 5: "'", 6: 'T', 7: 'V', 8: '8', 9: '?', 10: '%', 11: 'S', 12: '0', 13: 'u', 14: 'R', 15: '$', 16: 'd', 17: 'M', 18: '2', 19: 'F', 20: 'p', 21: 'b', 22: '-', 23: 'D', 24: 'y', 25: '.', 26: ':', 27: '(', 28: 'X', 29: 'o', 30: 'k', 31: 'j', 32: 'ç', 33: '@', 34: 'l', 35: '\n', 36: 'W', 37: 'C', 38: '5', 39: 'i', 40: 'O', 41: '6', 42: 'z', 43: '9', 44: ')', 45: '4', 46: 'G', 47: 'c', 48: 'A', 49: 'U', 50: 'L', 51: '*', 52: 'J', 53: 'x', 54: ',', 55: 'Q', 56: 's', 57: 't', 58: 'Y', 59: 'a', 60: 'g', 61: 'B', 62: 'e', 63: 'H', 64: 'q', 65: 'r', 66: 'K', 67: '7', 68: '3', 69: '!', 70: 'w', 71: '1', 72: 'f', 73: 'I', 74: 'E', 75: 'N', 76: 'h', 77: ';', 78: ' ', 79: '/'}
Then we create 2 dictionary to encode and decode a char to an int
Finaly we create a vector from a char like this:
The dictionary defined above allosw us to create a vector of size 61 instead of 256.
Here and exemple of the char ‘a’
The vector contains only zeros, except at position char_to_ix[‘a’] where we put a 1.
import numpy as np
vector_for_char_a = np.zeros((vocab_size, 1))
vector_for_char_a[char_to_ix['a']] = 1
print (vector_for_char_a.ravel())
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0.]
Definition of the network
This neural network is made of 3 layers:
- an input layer
- an hidden layer
- an output layer
All layers are fully connected to the next one: each node of a layer are conected to all nodes of the next layer. The hidden layer is connected to the output and to itself: the values from an iteration are used for the next one.
To centralise values that matter for the training (hyper parameters) we also define the sequence lenght and the learning rate
#model parameters
hidden_size = 100
seq_length = 25
learning_rate = 1e-1
Wxh = np.random.randn(hidden_size, vocab_size) * 0.01 #input to hidden
Whh = np.random.randn(hidden_size, hidden_size) * 0.01 #input to hidden
Why = np.random.randn(vocab_size, hidden_size) * 0.01 #input to hidden
bh = np.zeros((hidden_size, 1))
by = np.zeros((vocab_size, 1))
The model parameters are adjusted during the training.
- Wxh are parameters to connect a vector that contain one input to the hidden layer.
- Whh are parameters to connect the hidden layer to itself. This is the Key of the Rnn: Recursion is done by injecting the previous values from the output of the hidden state, to itself at the next iteration.
- Why are parameters to connect the hidden layer to the output
- bh contains the hidden bias
- by contains the output bias
Define the loss function
The loss is a key concept in all neural networks training.
It is a value that describe how good is our model.
The smaller the loss, the better our model is.
(A good model is a model where the predicted output is close to the training output)
During the training phase we want to minimize the loss.
The loss function calculates the loss but also the gradients (see backward pass):
- It perform a forward pass: calculate the next char given a char from the training set.
- It calculate the loss by comparing the predicted char to the target char. (The target char is the input following char in the tranning set)
- It calculate the backward pass to calculate the gradients
This function take as input:
- a list of input char
- a list of target char
- and the previous hidden state
This function outputs:
- the loss
- the gradient for each parameters between layers
- the last hidden state
Forward pass
The forward pass use the parameters of the model (Wxh, Whh, Why, bh, by) to calculate the next char given a char from the trainning set.
xs[t] is the vector that encode the char at position t ps[t] is the probabilities for next char

hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t-1]) + bh) # hidden state
ys[t] = np.dot(Why, hs[t]) + by # unnormalized log probabilities for next chars
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars (this is also called the softmax() function)
or is dirty pseudo code for each char
hs = input*Wxh + last_value_of_hidden_state*Whh + bh
ys = hs*Why + by
ps = normalized(ys)
Backward pass
The naive way to calculate all gradients would be to recalculate a loss for small variations for each parameters.
This is possible but would be time consuming.
There is a technics to calculates all the gradients for all the parameters at once: the backdrop propagation.
Gradients are calculated in the oposite order of the forward pass, using simple technics.
goal is to calculate gradients for the forward formula:
hs = input*Wxh + last_value_of_hidden_state*Whh + bh
ys = hs*Why + by
The loss for one datapoint

How should the computed scores inside f change to decrease the loss? We’ll need to derive a gradient to figure that out.
Since all output units contribute to the error of each hidden unit we sum up all the gradients calculated at each time step in the sequence and use it to update the parameters. So our parameter gradients becomes :

Our first gradient of our loss. We’ll backpropagate this via chain rule

def lossFun(inputs, targets, hprev):
"""
inputs,targets are both list of integers.
hprev is Hx1 array of initial hidden state
returns the loss, gradients on model parameters, and last hidden state
"""
#store our inputs, hidden states, outputs, and probability values
xs, hs, ys, ps, = {}, {}, {}, {} #Empty dicts
# Each of these are going to be SEQ_LENGTH(Here 25) long dicts i.e. 1 vector per time(seq) step
# xs will store 1 hot encoded input characters for each of 25 time steps (26, 25 times)
# hs will store hidden state outputs for 25 time steps (100, 25 times)) plus a -1 indexed initial state
# to calculate the hidden state at t = 0
# ys will store targets i.e. expected outputs for 25 times (26, 25 times), unnormalized probabs
# ps will take the ys and convert them to normalized probab for chars
# We could have used lists BUT we need an entry with -1 to calc the 0th hidden layer
# -1 as a list index would wrap around to the final element
xs, hs, ys, ps = {}, {}, {}, {}
#init with previous hidden state
# Using "=" would create a reference, this creates a whole separate copy
# We don't want hs[-1] to automatically change if hprev is changed
hs[-1] = np.copy(hprev)
#init loss as 0
loss = 0
# forward pass
for t in range(len(inputs)):
xs[t] = np.zeros((vocab_size,1)) # encode in 1-of-k representation (we place a 0 vector as the t-th input)
xs[t][inputs[t]] = 1 # Inside that t-th input we use the integer in "inputs" list to set the correct
hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t-1]) + bh) # hidden state
ys[t] = np.dot(Why, hs[t]) + by # unnormalized log probabilities for next chars
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars
loss += -np.log(ps[t][targets[t],0]) # softmax (cross-entropy loss)
# backward pass: compute gradients going backwards
#initalize vectors for gradient values for each set of weights
dWxh, dWhh, dWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
dbh, dby = np.zeros_like(bh), np.zeros_like(by)
dhnext = np.zeros_like(hs[0])
for t in reversed(range(len(inputs))):
#output probabilities
dy = np.copy(ps[t])
#derive our first gradient
dy[targets[t]] -= 1 # backprop into y
#compute output gradient - output times hidden states transpose
#When we apply the transpose weight matrix,
#we can think intuitively of this as moving the error backward
#through the network, giving us some sort of measure of the error
#at the output of the lth layer.
#output gradient
dWhy += np.dot(dy, hs[t].T)
#derivative of output bias
dby += dy
#backpropagate!
dh = np.dot(Why.T, dy) + dhnext # backprop into h
dhraw = (1 - hs[t] * hs[t]) * dh # backprop through tanh nonlinearity
dbh += dhraw #derivative of hidden bias
dWxh += np.dot(dhraw, xs[t].T) #derivative of input to hidden layer weight
dWhh += np.dot(dhraw, hs[t-1].T) #derivative of hidden layer to hidden layer weight
dhnext = np.dot(Whh.T, dhraw)
for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients
return loss, dWxh, dWhh, dWhy, dbh, dby, hs[len(inputs)-1]
Create a sentence from the model
#prediction, one full forward pass
def sample(h, seed_ix, n):
"""
sample a sequence of integers from the model
h is memory state, seed_ix is seed letter for first time step
n is how many characters to predict
"""
#create vector
x = np.zeros((vocab_size, 1))
#customize it for our seed char
x[seed_ix] = 1
#list to store generated chars
ixes = []
#for as many characters as we want to generate
for t in range(n):
#a hidden state at a given time step is a function
#of the input at the same time step modified by a weight matrix
#added to the hidden state of the previous time step
#multiplied by its own hidden state to hidden state matrix.
h = np.tanh(np.dot(Wxh, x) + np.dot(Whh, h) + bh)
#compute output (unnormalised)
y = np.dot(Why, h) + by
## probabilities for next chars
p = np.exp(y) / np.sum(np.exp(y))
#pick one with the highest probability
ix = np.random.choice(range(vocab_size), p=p.ravel())
#create a vector
x = np.zeros((vocab_size, 1))
#customize it for the predicted char
x[ix] = 1
#add it to the list
ixes.append(ix)
txt = ''.join(ix_to_char[ix] for ix in ixes)
print ('----\n %s \n----' % (txt, ))
hprev = np.zeros((hidden_size,1)) # reset RNN memory
#predict the 200 next characters given 'a'
sample(hprev,char_to_ix['a'],200)
----
,$KB?oFya2yGiNl*WGR3qC@.Cç
*yxçG4qioRAf/Bb*'
oqDtY"LE7,/:1/VU@u2@n"Oqç./K$@gt!Dn;UoS7w'n8c:@/RM8gLjb:gBX;ç)Rc4K*Ep!P?T"1f18;a@7,w0GRWC5'C$-2c4),Ej7-yxLTfB$zMihdHf(tiqlyx/ )/ Gyq4r)cw.H4$(ç-
I78nDF/CGg
----
Training
This last part of the code is the main trainning loop:
- Feed the network with portion of the file. Size of chunk is seq_lengh
- Use the loss function to:
- Do forward pass to calculate all parameters for the model for a given input/output pairs
- Do backward pass to calculate all gradiens
- Print a sentence from a random seed using the parameters of the network
- Update the model using the Adaptative Gradien technique Adagrad
Feed the loss function with inputs and targets
We create two array of char from the data file, the targets one is shifted compare to the inputs one.
For each char in the input array, the target array give the char that follows.
p=0
inputs = [char_to_ix[ch] for ch in data[p:p+seq_length]]
print ("inputs", inputs)
targets = [char_to_ix[ch] for ch in data[p+1:p+seq_length+1]]
print ("targets", targets)
inputs [40, 1, 62, 78, 2, 29, 65, 1, 39, 1, 60, 54, 78, 70, 76, 62, 1, 78, 46, 65, 62, 60, 29, 65, 78]
targets [1, 62, 78, 2, 29, 65, 1, 39, 1, 60, 54, 78, 70, 76, 62, 1, 78, 46, 65, 62, 60, 29, 65, 78, 11]
Adagrad to update the parameters
This is a type of gradient descent strategy

step size = learning rate
The easiest technics to update the parmeters of the model is this:
param += dparam * step_size
Adagrad is a more efficient technique where the step_size are getting smaller during the training.
It use a memory variable that grow over time:
mem += dparam * dparam
and use it to calculate the step_size:
step_size = 1./np.sqrt(mem + 1e-8)
In short:
mem += dparam * dparam
param += -learning_rate * dparam / np.sqrt(mem + 1e-8) # adagrad update
Smooth_loss
Smooth_loss doesn’t play any role in the training. It is just a low pass filtered version of the loss:
smooth_loss = smooth_loss * 0.999 + loss * 0.001
It is a way to average the loss on over the last iterations to better track the progress
Main Loop (Testing)
Here the code of the main loop that does both trainning and generating text from times to times:
n, p = 0, 0
mWxh, mWhh, mWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
mbh, mby = np.zeros_like(bh), np.zeros_like(by) # memory variables for Adagrad
smooth_loss = -np.log(1.0/vocab_size)*seq_length # loss at iteration 0
while n<=1000*100:
# prepare inputs (we're sweeping from left to right in steps seq_length long)
# check "How to feed the loss function to see how this part works
if p+seq_length+1 >= len(data) or n == 0:
hprev = np.zeros((hidden_size,1)) # reset RNN memory
p = 0 # go from start of data
inputs = [char_to_ix[ch] for ch in data[p:p+seq_length]]
targets = [char_to_ix[ch] for ch in data[p+1:p+seq_length+1]]
# forward seq_length characters through the net and fetch gradient
loss, dWxh, dWhh, dWhy, dbh, dby, hprev = lossFun(inputs, targets, hprev)
smooth_loss = smooth_loss * 0.999 + loss * 0.001
# sample from the model now and then
if n % 1000 == 0:
print ('iter %d, loss: %f' % (n, smooth_loss)) # print progress
sample(hprev, inputs[0], 200)
# perform parameter update with Adagrad
for param, dparam, mem in zip([Wxh, Whh, Why, bh, by],
[dWxh, dWhh, dWhy, dbh, dby],
[mWxh, mWhh, mWhy, mbh, mby]):
mem += dparam * dparam
param += -learning_rate * dparam / np.sqrt(mem + 1e-8) # adagrad update
p += seq_length # move data pointer
n += 1 # iteration counter
iter 0, loss: 109.550668
----
TMj*BNSn0yjY%W%g'BgU9Se%4?FOD:nqc23ck?M!(nd/cqS3Uç2
-4PY-dK!D.f6y:A'bE9gcmUn)zKokHwo'IDATmFmc0 *Sdfve*CgnNh""N3()JsYHy"Jw
1dVvHXb-u9"7I6'fx@IV:bçv.:K0m-$mc9gP-EPzWqJunNPcge8ROaj2"O
nI 1'DK("$W7"JTRTDg
----
iter 1000, loss: 85.422755
----
ho,d in hie. oft the is he Pk dim Se Yha sed hirg cor f.o ghenlim letop cf dGr faapo ghe Bt sT fo ve yat ek le ago herig fee chiughe lriny he fin iick ih hik her thk time tl me ho be n,ig doml, hre
----
iter 2000, loss: 68.049943
----
rk wo-y ver, fhey mimeregstthorpere, -he hering omwars fuske whed toof. ther; deind 'ror saves Auons he Grorks wour -r dswh mhot an. Hsuthers wacser. way horewank the hemed maid the come hoitinhat, wa
----
iter 3000, loss: 59.226622
----
tremhemror hisrest bubingon und intheusjd an opnkly and a;ofures bbegy hos we ss thouly tve hart ares thet; buos heryd w; wisnse rouskthe somcpung pegtey, sted uy his dofrack hist bhid hiet pne hek go
----
iter 4000, loss: 54.907025
----
I sors so to al wsowkiwh hon atteackry ap and his Theumpith thvey Irint nowadit chay ay thound or hinang mame ir ow wawave to woolimerion wnowithing aither othar Grered. rat for bieiskye And camle to
----
iter 5000, loss: 56.720454
----
e 1ion at persey pnruce worke at iomeledingop Gne isronecto btLseafut) wiok. EenE -rthErjEGre
ed ofrecrrostanit cio tgry Sroug Growhotudsadesut; ticke Us cp ine yrradked
1ouk.
p1rs sornar the gores.
1
----
iter 6000, loss: 57.245813
----
he fomen futh anccersem ond cuon anfund newer hand and be thand morimealde ratiove to he wou forn Gutk an clund sor nas to walle to yoting sapento pivey bowwe theing reven the d the ate pith mamparad
----
iter 7000, loss: 53.229863
----
reg mow thetrast hay pithe the tis bound to thingo time nealathe thet he his hap woomensy and he wledis her to wavedis im gapam. wasicke to toom Grevicto costing all sexabe
eroperlicd on the .ad has
----
iter 8000, loss: 50.293759
----
sco sho lecle, to as ould ssecfenk coin the sleples ef deen. Gregor thet peeut thely him stomed titheling ofly hivest, a letk, the beckelfef wone to rett. gent if on the to has aldast oulo vitto nooly
----
iter 9000, loss: 48.924231
----
ainitheresukededpsoit rite absupeencay sistoft hases fathiacken, beit seottang; deeriog tiononcver eveir ot ef theibeas that himast, en, anis. difrrracfusingorg seast.
Abengingout kither, to cong out
----
iter 10000, loss: 48.367904
----
of cror se lonbthant notinged toming ssers rot inlsanede fithe the waaked wore of bas to the faon then tunf. Weill buteanl. lemod furfed, the lonthiso tored theughly wurgieg roome gandsisser "singald
----
iter 11000, loss: 54.611887
----
. WImenquess inraly ouce
Projertexle worp
tE thipsrith un us of pfuntitmedrov ig and com wishy ssom
aisecat of Prqueptey bestiGr, a
cas6, thpackangening, Sheamed./TWnont Prranm. itericpmser. Mr's chu
----
iter 12000, loss: 51.542726
----
the low of was leens.
Ss thy ove feat - clier, it a wnehs a ptecs gond stid, GreiO string wem. Gregtasndat dohist westhithipit. He bay he roffrvey yal mang for he the kling made to he
sire peeen in th
----
iter 13000, loss: 48.520714
----
oontert,onde dimd, go realy. Grelas him the forest he had of that oray cons soot mo her to it out geare mast if his your hom wit froughe's roommengh that whe ferseek in the shoterith anling leded whod
----
iter 14000, loss: 46.730923
----
plowpersing not sess, chanding froughtideer thuur and aly eiftrhad wretelp." onterret ioly was whpt st wur sehtiegle; in his spr it oltunsting in now tantething mramre sade asm himist at out in to st
----
iter 15000, loss: 46.130857
----
eat for atrathinges toraneaply mure tith in vert; havink sighted therse in the afCaln that they ked tad the k hin to birk to maken ansttrilly him that row ofreg atyet thre dmather's wime le anank even
----
iter 16000, loss: 48.502561
----
ien of lion Usly warc or note.
And fonmovimeating (ork in that cromested; wirk outd Guticinis look poustsed et the dimpy
lisicthin) 'sintiagade, (oucly distered ifsing. ne not of at ait perte alings
----
iter 17000, loss: 50.239302
----
he bouch ked in woupef inclienomaght to bacl perere orecin mocl of that canrotice cawhor'sirgewos laken. . Thert have holl not tion buca wom comend wookseS. Anky ofden then be the him the ro his of wo
----
iter 18000, loss: 47.724164
----
t queymares readly aimper all, Gregor prow ta tore spry. Way Gregond be ast, him! ighwas ssoscy at the farisidheading out as the far mo porithear prrectly now of work as ibredenteind buce toout woukde
----
iter 19000, loss: 45.661126
----
std shatr ar from hathem his lessey thad it lowould of sher of this at his cousd it quingand larls had ang flomy be hos hos net houre thod's bectey loter and wave, by litist his twoughtlonesteverpient
----
iter 20000, loss: 44.939163
----
to chirtmeang tide agent was - and to got one even the wacj, lled mame quck the do lumed becaly a grerlivereded her whels had rot ont, boun whan him it himevorl nith yishing the fat alt's simin, evel
----
iter 21000, loss: 44.791554
----
d toursishent was eakener anthisey they about tarker, she had rea taftmon to itgetwayed busferaing her lhe some was helfoon thied his she forengerto wathoure outel foresidide sist rat wather llay the
----
iter 22000, loss: 49.407495
----
ls Alle forld
bute arlathar of and of Youccerl be if e lolrathect Gregor. I chimed cotpound oven thisatpar on
corclibeced lass a weid wossaticutecatee or'clasibens lefungo a pron ever of Profeamifabr
----
iter 23000, loss: 47.633807
----
elt in't wouming the he was, him; becser theak camermed you cousthe have watl. 8nd was all himwads. Ont out wit thathiat he what that no parens. The pithly slent not. Whaterged pare.t he hed dieth! An
----
iter 24000, loss: 45.416383
----
k Gregor fornst had a sle lesser propan de knaup. Ity at sared, hat hot enevel wher of the sparbly quism faker ould sormen whin ofe qued the wound elong, hius thon her her creen be coufth to by f a fr
----
iter 25000, loss: 43.957373
----
ediass wion wachen to shas wath and hour at sustheredy out in tufterming pouls gather the didlele Gregor abligen piuld backs imen hos have the cleded pighty ulle agest but Gringury, roach. Whiss. Styt
----
iter 26000, loss: 43.589324
----
cen alinf tevere her with I raile from the the difle , just had sluning showed and reimy; was the his sate, andint, lend it sert grangenfetive to when, cwhur brest staroinhart wasked clevillle frot fa
----
iter 27000, loss: 45.546408
----
ut Pre for this Qneng tcreatedbre for oricrenty im, pured mon the styo that hade tat thin Prreg it Project, work reca ouch U tuUt brouner work. Sh ofsale Pr jig-tperted in conite tley care"
Projaon on
----
iter 28000, loss: 47.457231
----
SI he all chas, a polainid and mande and soorm for wound he Shovers makseray bred on (ou tabeee had it mis, ur the prizele be a bay be the dom sook a to him thing bromatine didatite mover, groy he wa
----
iter 29000, loss: 45.450032
----
thear. So his oft dit wsicsive at not backs Gregor werce to his woocto befor youtad soor was quive and torfith oftenturoakgoumy wittontunt to from by of under wishent of all, and asy that not room ont
----
iter 30000, loss: 43.655464
----
ondy cleasid to bref his disce and anxaon, entered.
Brelyr.
Gregor's weat he wapg sthey we had abrive a
thirr as nich sither the saetent and fitterttle the couls bequettly pare would lee or he see c
----
iter 31000, loss: 43.123554
----
mudevid and ulame Gregor her hove he lat Ir: to fat othen to he wan elped a proused tion in heas soow thin to she dore mont out enther as doormegias nimen of - him to but as ofbed fat wat tely make du
----
iter 32000, loss: 43.019857
----
ooned lout foll inss to he hade there was- bat she his same it wime at timle istended to her no, vooder of the his hin out htmed and shot in thin the out whind nid tamet inthridce, Cotling, anl she ch
----
iter 33000, loss: 47.131538
----
yy ubdarrangreftunberg-tP of eleenension fors. 3 abain aratwaded of the Ditedarccost ableve, a wo forommin of toning Thruch warts
a chatiobly.
The coffen that Unat: I
Sarnocce
1450it - this of varpr
----
iter 34000, loss: 45.836815
----
forg wwiry ny tery if he dod the forwaid ence sufinnopd, chaid sams, youp to hared thin have be anding if then to iught, aly.
The had from while samet the cous her so sufind eserietily morento, sxedn
----
iter 35000, loss: 43.800318
----
t bes, mute strud talced tumeveryed to on e's agative would go stele, alded way he beer. That the od that I was , slets caily fiever, yenisy very a'kly lose stose sleed to had while; rever of most. Sa
----
iter 36000, loss: 42.489710
----
ed, lactont as heme "Green is bespict his hotesidbem it would, and weon as tha woully on blaide they it had but aghing and fiele; thinesent have thay sestGregor get's too smow his Same abanly, him eve
----
iter 37000, loss: 42.251025
----
wothtever, jusd to merunely whokiling in hanwonwouding was most on eacchiagreded wousted as gorideon, is hanf ore the rooiny hay moreeor bore it could fork, had futing ond in same was wooncem weet but
----
iter 38000, loss: 43.953440
----
or
you coupge"
Projechevinntetsowlawo couy (
regsistecle any no costeced abound where commed the to wikning arcopens
Protcout caned alres in meceesle thisypiobeaten, pustitestary whane to Projemt en.
----
iter 39000, loss: 46.452669
----
selachinf a slich sappes Bored at./And oulld in to shen kidess
un thund had corded his at ingor withed to buck ad but. But and . He to bed. Gregor ged the pitht he wat liti. Gut. SMort oud he he luc
----
iter 40000, loss: 44.345093
----
acred that tallay. I dey anyid'mse a mat samied it down hain his to sister, the him to beall. litine and by was notust, pitt the pain baade and sain he was staken all, of having and thingery on urme i
----
iter 41000, loss: 42.554754
----
pely hey indous tpigame thought flould almongowfed and to womle as would him all, cound thet g loot nilliass to ro lvere; all ther foor and noly, stppop.
nowned tigle froolable beenger whire one and
----
iter 42000, loss: 42.077433
----
y of the swever, in takilise, pley sact waftle a bed tenome ankine wime back silles mothough miccoun him a almimp ouse his sowest weld, hoct to to was rethe heaced betse to and of wibls als. feas, and
----
iter 43000, loss: 46.777936
----
the at wife. Ave Dlist here hime gitumand, if the Fook lithisy sicee enely allas simowe sesteale ind hark dent the wit wap hist hime nime nod wat ance Saching ar. Her 1ice nound toul thingonglade" me
----
iter 44000, loss: 53.759189
----
alloroninnised on efomest thate, motto cho the oudsenticcratreOn ancert
wacr sle.
5
N
doungnfe dont, torm withe peemuspenat conana c sven do moclede lamincede fofe cadnevs
Drred and quertsow ounge
----
iter 45000, loss: 49.034741
----
d eruit they coull celiate becouse the roomag!
"Whamtecing paren mo cerr noving anes "A'k was ed the come muth of Bs with had jast that the as a any seong this had the there enterrty ond to he hear ha
----
iter 46000, loss: 44.633663
----
ttond and rus goot that his houldlywly acls at dit leare the bode's dexs, ind amy to if the saying the drebus somearlyst to about even his the tome, heys, plome the marmayy at on them. On'me mathem in
----
iter 47000, loss: 42.406129
----
futlined have un the dear thinged and onadens dod stard with and fithorted the plethey stestid he wapthing the father, and thred, able "balke shirsed theil. He daving, and he said, ull, evinest "no wa
----
iter 48000, loss: 41.796630
----
sw she was prat wour shand the for so eace to sighame him long thres, his on worms, traich wat whand and was dey the the his was fathaich hay ple hoy espmsing she doof srom sroould to thising and for
----
iter 49000, loss: 43.580185
----
hold rooll ant by any ley aropprease you pornateod worksely, Uno lonpstersed plen she ty tainemed the cotedred" Abrabl, to she in enberchimation owiwe fregorsedr.
Propidys at thred ugeanct kerse, ing
----
iter 50000, loss: 45.491333
----
nate of futher he dot contitcely to your?" ASce foous bodidgoreny she doo havinbo requening ig-tnos to lomene becwastutecens was soaker learus unatef eest in deal tright beer of the roo, even hement,
----
iter 51000, loss: 43.577728
----
father had the frequing quede to morenbely and lisal that his leavation. could betinf c niatget diche from to know as of tothat was some and tion., Gregor if had werey tmey, and on the entucouth to t
----
iter 52000, loss: 41.844923
----
f would rivane, inly fest entlidedly all of the shatled the prigenting of the jovesting!/ her for have had provled of his Gregoble capion lil his beafsed and would and it ta fire ofd, dof ubrect reigh
----
iter 53000, loss: 41.492205
----
long thiugh them worked she hered it there was that her anyso mothen had ot that, him ne them doon him, the was the stet had awaid was though that shorm the did itsert, becers door tuy; cuther he vear
----
iter 54000, loss: 41.381327
----
and said him movieg wasired to her that of ae" soon did sect have, want beass stome fles of out.
The chaw timere had be aspent than Madioun fake. He so move to in all; imsed hoake: "out his juen one
----
iter 55000, loss: 45.114489
----
ed this dot.
1.E. wert on oom where collly expy p:Nock abrient fullotend. Liss on in a tive soprain capores Projed warsailn the he
. Sestarbont, sprinfor'berforned of umanang: Pricemenf fole from i
----
iter 56000, loss: 44.096006
----
e hather had their effentow the more, all as immain, at sreanss pare" to be of undenting. Shang, brises of ther had wast a yound cher, did, uf unting thinger, he hould hising lent then st he wack in w
----
iter 57000, loss: 42.199812
----
so by iughely. 9ed as he cafly pighroms but door. niven weliss the brengeven, undongers would the ald any doon couldw werd bray paide open he voich deesent genteroming and on uf fit -o was wass allys
----
iter 58000, loss: 41.038218
----
sheve other back all thatgelist inge, about of the as had his, the reaktevery he had uporning but, so hin the dife come, twabers innle was her stunten. He was eland; fhow himw busing the an edow:, fr
----
iter 59000, loss: 40.816907
----
escever.
"Wh agd sas lefthen Green, beheyor'w the chaip, arms unespitelalrcem bectint ther, her by surment a they alrould nicisme, the gond, dus bus arably as atidloame even or ovelf, had he could co
----
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
<ipython-input-20-834c7c41fd8f> in <module>()
13
14 # forward seq_length characters through the net and fetch gradient
---> 15 loss, dWxh, dWhh, dWhy, dbh, dby, hprev = lossFun(inputs, targets, hprev)
16 smooth_loss = smooth_loss * 0.999 + loss * 0.001
17
<ipython-input-15-e436d91b06b9> in lossFun(inputs, targets, hprev)
27 xs[t] = np.zeros((vocab_size,1)) # encode in 1-of-k representation (we place a 0 vector as the t-th input)
28 xs[t][inputs[t]] = 1 # Inside that t-th input we use the integer in "inputs" list to set the correct
---> 29 hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t-1]) + bh) # hidden state
30 ys[t] = np.dot(Why, hs[t]) + by # unnormalized log probabilities for next chars
31 ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars
KeyboardInterrupt:
